“Comprehensive Question”

Q NO 1: State and explain Newton’s law of universal gravitation. Also show that it follows Newton’s third law of motion.

Answer :

Newton’s law of Universal gravitation:

This law was proposed by Sir Isaac Newton.

Statement:

This law states that ” Everybody in the universe attracts every other body with a force known as force of gravitation. This force is directly proportional to product of masses of bodies and inversely proportional to square of distance between their centres.”

Explanation:

Consider two bodies having masses m₁ and m_2.Distance between their centres is ‘r’ as shown in figure.

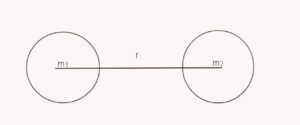
According to Newton’s law of Universal gravitation, both masses will attract each other with a force of gravitation Fg  which is given by ,

Fg  ∝ m₁m₂    …….. (i)

Fg  ∝ 1/r²      …….. (ii)

Combining relation (i) and (ii)

Fg ∝ m₁m₂/r²

Fg = Gm₁m₂/r²

Where G is constant of proportionality known as Gravitational constant. Value of G as determined experimentally is 6.67 × 10^-11Nm² / kg².

In Newton’s law of universal gravitational both bodies act forces on each other. These two forces are equal in magnitude but opposite in direction.

F₁₂ = -F₂₁

Example:

Earth pulls on the moon with a force, the moon pulls on the earth with a force of equal magnitude but opposite direction.

Earth pulls an object of mass 1.0 kg with a force of 9.8N. The object also pulls on the earth with a force of 9.8 N.

• Show that Newton law of universal gravitation follows Newton’s third law of motion.

Answer :

               In Newton’s third law of motion action and reaction forces act on each other. In Newton’s law of universal gravitation force acting on mass m1 due to mass m2 is F12. Also , force acting on mass m2 due to mass m1 is F21. These two forces are equal in magnitude but opposite in direction.

F₁₂= -F₂₁

We can say that these two forces action reaction forces because action reaction forces are also equal in magnitude but opposite in direction. So Newton’s law of universal gravitation follows Newton’s third law of motion.

Q NO 2: Determine mass of earth using law of Universal gravitation.

Answer:

            We can find Mass of Earth with the help of law of universal gravitation.

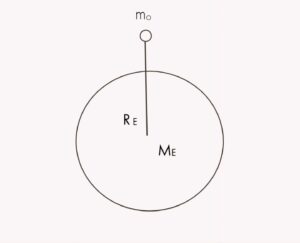
Explanation:

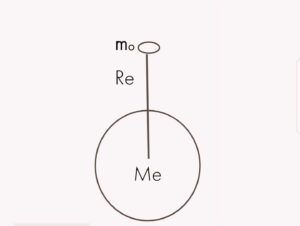
Consider an object of mass m_o is placed near the surface of earth. Let the mass of earth is Me . The distance between object and centre of earth is almost equal to radius of earth Re.  Two forces will be acting on the body. First by Law of universal gravitation the force of attraction between object and will be given by,

Fg = Gm_oMe/ Re²     ……… (i)

Second force acting on the body is force of gravity which will be equal to weight of a body.

Fg = w = m_og             ………. (ii)

Comparing equation (i) and (ii)

m_og = Gm_oMe/ Re²

g = GMe / Re²

gRe² = GMe

Me = gRe²/ G

Above equation shows that mass of earth depends upon gravity of Earth, the radius of Earth gravitational constant G.

We know that , g_e= 9.8 m/s²

Re = 6.4 × 10⁶ m

G = 6.67 × 10^-11Nm²/kg²

Putting these values in above equation ,

Me = (9.8 ms^-2 × 6.4 × 10⁶ m ) / ( 6.67 × 10^-11 Nm² / kg² )

Me = 6 × 10²⁴ Kg

The formula for mass of earth is universal formula . We can find Mass of any astronomical object with the help of this formula.

Q NO 3: What is gravitational field and gravitational field strength. Show that weight changes with location.

Answer:

• Gravitational field:

                   The region around mass where it can exert force on another mass is known as Gravitational field. A gravitational force is attraction force of a mass and gravitational field of another mass. Similarly the region around Earth where it can exert force and any object is known as gravitational field of earth.

• Gravitational field strength:

                      The gravitational field of Earth at any point around Earth can be described by gravitational field strength ‘g’. The value of g is equal to the magnitude of gravitational force acting on a object of mass 1 kg.

g = Fg/m

• Show that weight changes with Location.

Consider an object (e.g a cricket ball ) of mass m_o is placed on the surface of earth with mass Me. Re is distance between centre of object and earth. Two forces are acting on this object. The gravitational force between earth and cricket ball will be

Fg = Gm_oMe/ Re²    ……… (i)

The gravitational field strength is given by ,

Fg= m_og                     ………. (ii)

Comparing both equation i and ii

m_og = Gm_oMe / Re²

g = GMe/ Re² …… (a)

As G = 6.67× 10^-11 Nm²/ Kg²

Me = 6 × 10²⁴ kg

Re = 6.4 × 10⁶ m

Putting values,

g = 6.67 × 10^-11 Nm²/kg² × 6 × 10²⁴ kg / (6.4× 10⁶m)²

g = 9.8 m/s²

The above equation of gravity can be generalized as

g = GM/ R² ….. (b)

We can find the value of gravity on any astronomical object with the help of this formula if we know it’s mass and radius.

• Above equation shows that the value of g does not depend upon mass of body so heavier and lighter objects for towards earth with name acceleration.
• According to this equation value of g only depends upon mass of earth and radius of earth. As Earth is not perfectly the sphere shape. It has mountains and trenches etc, so the value of varies with location on earth . As weight is dependent upon the value of g so it also changes it location with g.

Q NO 4 : How is value of g changes with going to Higher altitude. Give relevant formula.

Answer:

           The value of g at the surface of any astronomical object e.g earth is given by,

g = GMe/Re² …. (i)

where Me is mass of earth and Re is radius of object.

The value of g at any point on the surface of earth depends on the distance from the centre of earth . Greater the distance from the centre of earth smaller will be value of g. Let ‘gh’ be acceleration due to gravity at height h then above equation becomes

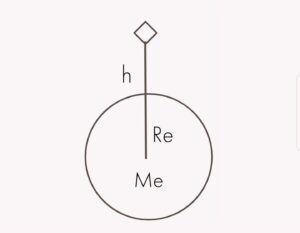
     g_h= GMe / ( Re+h)² ….(ii)

As we know ,

g = GMe / Re²

So , gRe² = GMe …… (iii)

Putting value of GMe in equation ii

g_h = gRe² / (Re+h)² ……. (a)

Above equation shows that when we move away from the centre of earth at any height the value of g decreases.

Q NO 5: Derive formula for orbital speed of satellite.

Answer :

Satellite:

            A satellite is man made or naturally occurring object that revolves around another object due to force of gravity. e.g moon is natural satellite of earth and earth is natural satellite of Sun.  

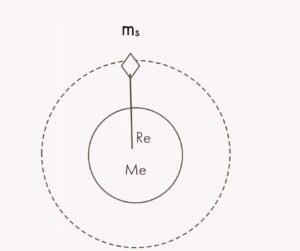
Speed of satellite:

                      When a satellite is moving in around the earth it has constant orbital speed. Consider a satellite of mass ms is moving with velocity v in orbit around earth of mass Me. Let r is distance between centre of earth and satellite . Two forces are acting on satellite . The gravitational force between earth and satellite is given by ,

Fg = GMem_s/r² ……… (i)

Satellite moves around Earth due to centripetal force. This centripetal force is given by,

Fc = m_sv²/r ……. (ii)

Comparing equation i and ii

m_sv²/r = GMem_s/r²

v² = GMe /r

√v² = √GMe/r

v = √GMe/r        ………. (a)

This equation shows that the speed of Satellite is inversely proportional to distance between centre of earth and satellite. That means satellite near the earth will have greater Velocity.

“Numerical Questions”

Q NO 1: Pluto’s moon Charon is unusually large considering Pluto’s size , giving them the character of a double planet. Their masses are 1.25×10²² kg and 1.9×10²¹ kg , and their average distance from one another is 1.96×10⁴km. What is gravitational force between them?

Given data:

mass of Charon = m_c= 1.25×10²² kg

mass of Pluto = m_p = 1.9×10²¹ kg

Average Distance= r= 1.96×10⁴km = 1.96×10⁷m

Gravitational constant= G = 6.67×10^-11Nm²/kg²

Required:

Gravitational Force= Fg = ?

Solution:

We know that gravitational force between Pluto and charon is given by,

Fg = Gm_pm_c/r²

Putting values ,

Fg = 6.67×10^-11×1.25×10²² × 1.9×10²¹ /(1.96×10⁷m)²

Fg = 15.8 × 10³² / 3.84×10¹⁴

Fg = 4.1 × 10¹⁸ N

Q NO 2: The mass of Mars is 6.4×10²³ kg and having radius of 3.4×10⁶m. Calculate the gravitational field strength (g) on Mars’s surface.

Given Data:

mass of mars = Mm = 4.6×10²³ kg

radius of mars = Rm = 3.4 × 10⁶ m

Gravitational constant= G = 6.67×10^-11Nm²/kg²

Required:

Value of g on Mars surface= g_m = ?

Solution:

We know that value of g is given by ,

              g = GMm/Rm²

g = 6.67×10^-11 × 4.6× 10²³ /(3.4×10⁶)²

g = 42.7× 10¹² / 11.56×10¹²

g = 3.68 N/kg

Q NO 3: Titan is the largest moon of Saturn and the only moon in the solar system known to have a substantial atmosphere. Find the acceleration due to gravity on Titan’s surface if it’s mass is 1.35×10²³ kg and it’s radius is 2570 km.

Given Data:

 Mass of Saturn = Ms = 1.35×10²³ kg

Radius of Saturn= Rs= 2570 km = 2570×10³ m

Required:

     Acceleration due to gravity= g = ?

Solution:

 We know that value of g is given by ,

                     g = GMs/Rs²

g = 6.67×10^-11×1.35×10²³ /(2570×10³)²

g = 9.0×10¹² / 6.6× 10¹²

g = 1.36 m/s²

Q NO 4: At which altitude above Earth’s Surface would the gravitational acceleration be 4.9 m/s²?

Given Data :

            gravity at height= g_h = 4.9m/s²

Required:

           Height = h= ?

Solution:

We know that , the value of gravitational acceleration at any point on height is

g_h= g_eRe²/ (Re+h)² ….. (a)

g_h × (Re+h)² = g_eRe²

(Re+h)² = g_eRe² / g_h

√(Re+h)² = √(g_hRe² /g_h)

Re+h = √(g_eRe² / g_h)

h = √( g_eRe²/ g_h ) – Re  …….   (b)

Putting values ,

h = {√ (9.8ms^-2 × (6.4×10⁶m )² / 4.9ms^-2) – (6.4×10⁶m)

h = 2.6 × 10⁶ m

Q NO 5: Assume that a satellite orbits Earth 225 km above its surface. Given that the mass of earth is 6×10²⁴kg and radius of earth is 6.4×10⁶ m , what is satellite’s orbital speed?

Given Data:

mass of earth = Me = 6×10²⁴ kg

Radius of earth= Re = 6.4×10⁶m

Height of Satellite= h= 225 km = 225×10³m

Required:

     Orbital speed of satellite= v= ?

Solution:

            We know that orbital speed of satellite is given by,

v = √GMe/Re+h

Putting values ,

v = √ 6.67× 10^-11× 6×10²⁴ / ( 6.4×10⁶+225×10³)

v = √6.04×10⁷

v = 7.77× 10³ m/s

Q NO 6: The distance from centre of earth to centre of moon is 3.8 × 10⁸ m. Mass of Earth is 6 x 10²⁴ kg , what is orbital speed of the Moon?

Given Data:

Mass of earth= Me = 6×10²⁴ kg

Distance from centre of earth to centre of moon = r = 3.8×10⁸ m

Gravitational constant= G = 6.67×10^-11Nm²/kg²

Required:

Orbital speed of moon = v = ?

Solution:

         We know that Orbital speed of satellite is given by ,

                  v = √GMe / r

                  v = √ 6.67×10^-11× 6× 10²⁴ / (3.8×10⁸)

v = √10.5×10⁵

v = 1.02×10³m/s

Q NO 7: The Hubble space telescope orbits Earth of mass Me = 6×10²⁴ kg with an orbital speed 7.6 x 10³ m/s. Calculate it’s altitude?

Given Data :

Mass of earth = 6×10²⁴ kg

Orbital speed = v = 7.6× 10³ m/s

Required:

Height of satellite= h= ?

Solution:

 We know that orbital speed of satellite is given by,

           v = √GMe/Re+h

           Taking square on both sides

v² = GMe/Re+h

v²(Re+h) = GMe

Re+h = GMe/v²

h = (GMe/v²) – Re

h = {6.67×10^-11×6×10²⁴/( 7.6×10³ )²} – 6.4×10⁶ m

h = 6.93×10⁶ – 6.4 × 10⁶

h = (6.93-6.4) × 10⁶ m

h = 0.532 × 10⁶ m

h = 532 × 10³ m

h = 532 km

Click Here for Related Posts