Class 9th
Physics
Chapter 06
Work & Energy
Student Learning Objectives (SLO)
-
Work | Definition | Mathematical equation | Maximum work | Minimum work :
When a force is applied on an object and it covers some displacement in it’s direction, work is done on the object.
This definition of work is different from daily definition of work. For work in Physics force must be applied on the body and body should cover some displacement/distance.
- Mathematical Form :
If we exert a force F on an object , and it covers displacement S then work is done on the object and defined as force times displacement.
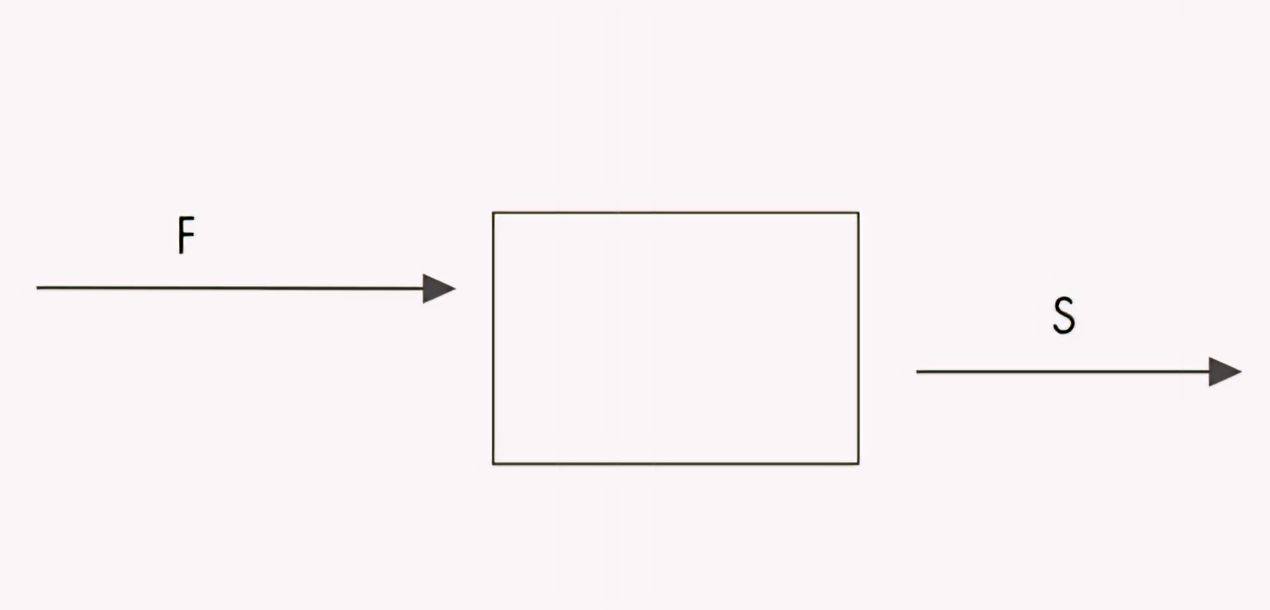
Mathematically,
work is given by,
w = F.s
Unit of work :
The unit of work is
w = F.s
w = Newton . metre
w = Joule
The S.I unit of work is Joule ( in honour of James Joule ) . Joule is equal to N.m.
1 J = 1 N × 1 m
SLO Question:
-
How unit of Work Joule is defined ?
Work is said to be 1 Joule , when 1 N force displaces a body to a displacement of 1 m.
1 Joule = 1 Newton × 1 m
-
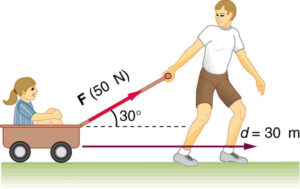
How work is calculated when force is applied at an angle?
As work is dot product / scaler product of force and displacement,
w = F.S
Force is not always parallel to displacement when force is applied at an angle it has two components. We know that horizontal component of force is responsible for obtained quantity from scaler product. So we will take Fx component of force .
w = Fx. S
w = Fcosθ × S
w = FScosθ
From above equation shows that work depends upon force applied displacement covered and angle between force and displacement.
Maximum work :
Work done will be maximum when force and displacement are parrell to each other or making an angle of 0° .
w = FS cos 0°
w = FS (1) : cos0° = 1
w = FS
In this case work done will be maximum.
Minimum work:
Work done will be minimum when
- i) Force is zero .
- ii) Displacement is zero.
iii) When angle between force and displacement are perpendicular to each other or making an angle of 90° with each other.
w = FS cos 90°
w = FS (0) : cos90° = 0
w = 0
No work is done when force and displacement are perpendicular to each other.
-
Does earth ever do work on Moon?
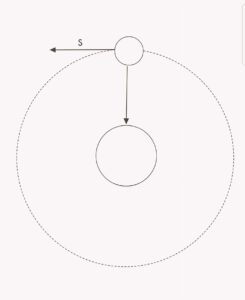
No, earth doesn’t do any work on Moon. Earth pulls on the moon with gravitational force towards itself. So the direction of force is towards earth. But the moon covers displacement tangent to its Elliptical path. So force and displacement are perpendicular to each other.
w = FScosθ
w = FScos90°
w = FS(0) , As cos90° = 0
w = 0
So no work is done by earth on the moon.Infact no Centripetal force can ever do work on an object.
-
Show that work is dot product of force and displacement.
We know that work is given by ,
w = F.S
Work is a scalar quantity we know that when two vectors are multiplied and a scalar quantity is obtained it is known as scalar product .As work is obtained by multiplying two vectors force and displacement so it is a scalar product or dot product of force and displacement.
Example 6.1
A person pulls a suitcase through the airport at 45° angle. The tension in the rope is 20N. How much work does the tension do if the suitcase is pulled 100m?
Given Data :
Tension in the rope = Force applied= 20N
Distance = S = 100m
Angle between force and displacement= 45°
Required:
Work done= w = ?
Solution:
By definition of work we know work is given by ,
w = FScosθ
Putting values ,
w = (20N)(100m)cos45°
w = 2000 Nm × 0.707
w = 1414 Joule
Because person pulls the rope , so person does work on the suitcase which is 1414 Joule.
Assignment 6.1
-
During a tug-if-war , team A pulls on the team B by applying a force of 1100 N to the rope between them. The rope remains Parrell to the ground. How much work does team A do if they pull team B toward’s them at a distance of 2.0 m?
Given Data :
Force = F = 1100 N
Distance = S = 2.0 m
Since the rope is parrell to ground so angle will be 0°.
Required:
Work done = w = ?
Solution:
Since by definition of work ,
w = FScosθ
Putting values ,
w = 1100N × 2.0 m × cos 0°
w = 2200 N.m × 1
w = 2200 N.m
w = 2200 Joule
So team A does 2200 Joule work on team A .
Related Example about work done
A boy pulls on the cart attached to a rope parrell to the ground such that tension in the rope is 150 N . The work done on the object is 3000 N . How much displacement body has covered?
Given Data:
Tension in the rope= Applied force on the object = F = 150 N
Work done on the object = w = 3000 J
Required:
Displacement= s= ?
Solution:
Since the force applied is Parrell to displacement so angle will be 0° and cos 0° = 1 so the work done will be given by ,
w = F • s
s = w / F
s = 3000 J / 150 N
s = 20 m
If a cart is pulled with a force of 150 N and work done is 3000 J then it must cover 20m displacement.
Frequently Asked Questions
2. What is the unit of work in S.I base units?
The unit of work in terms of base units is kgm²/s².
3. When work done will be maximum and minimum?
Work done will be maximum when angle between force and displacement is 0° and minimum when angle between force and displacement is 90°.
4. Who is doing more work ? A student running in ground or a teacher sitting on the chair and solving physics problems?
A boy running in ground is doing more work because he is covering displacement. On the other hand teacher is sitting on the chair is covering no displacement so no work is done in this case.
5. Why work done by centripetal force is always zero?
The work done by centripetal force is zero because in case of centripetal force the angle between force and displacement is 90° so no work is done in this case.
Kinetic Energy | Mathematical formula Derivation| Examples | SLO Questions
